無限反復指数関数の積分

以下の関数は、Infinite Power TowerやIterated Exponentialと呼ばれる関数です。日本語での定まった名称はありませんが、ここでは無限反復指数関数と呼ぶことにします。

$y=x^{x^{x^{x\cdots}}}$

一見不気味なこの関数ですが、実は $e^{-e}\leqq x \leqq e^{\frac{1}{e}}$ の範囲で収束することが知られており、その収束値は

$\displaystyle x^{x^{x\cdots}}=\frac{W(-\ln x)}{-\ln x}$

です。ただし $W(x)$ はランベルトのW関数( $y=xe^x$ の逆関数)です。

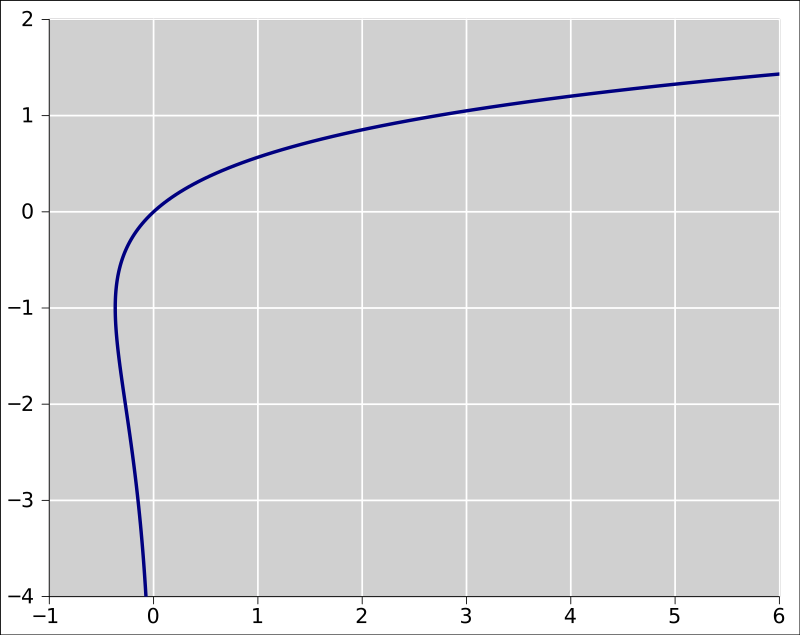
また、 $y=x^{x^{x\cdots}}$ $(e^{-e}\leqq x \leqq e^{\frac{1}{e}})$ のグラフは以下の通りです。

定積分を求めてみる

この関数を収束範囲いっぱいで積分してみます。
つまり $\displaystyle \int_{e^{-e}}^{e^{\frac{1}{e}}} x^{x^{x\cdots}} dx$ を求めてみます。

以下、 $f(x)=x^{x^{x\cdots}}$ として、 $f(x)$ の逆関数を求めてそれを利用します。

$y=x^{x^{x\cdots}}$

は、 $x$ の上に再び $y(=x^{x^{x\cdots}})$ が乗っていると考えることが出来るので、

$y=x^y$

をみたします。
これをxについて解くと、

$x=y^{\frac{1}{y}}$

xとyを入れ替えると、

$y=x^{\frac{1}{x}}$
$\ \ =\sqrt[x]{x}$

これが $f(x)$ の逆関数です。

グラフを書いてみましょう。
青線が $y=f(x)$ $(e^{-e}\leqq x \leqq e^{\frac{1}{e}})$ 、赤線がその逆関数 $y=x^{\frac{1}{x}}$ $(\frac{1}{e}\leqq x \leqq e)$ で、青い部分が求めたい面積(定積分)です。

青い部分の面積は、以下の赤い部分の面積に等しいです。

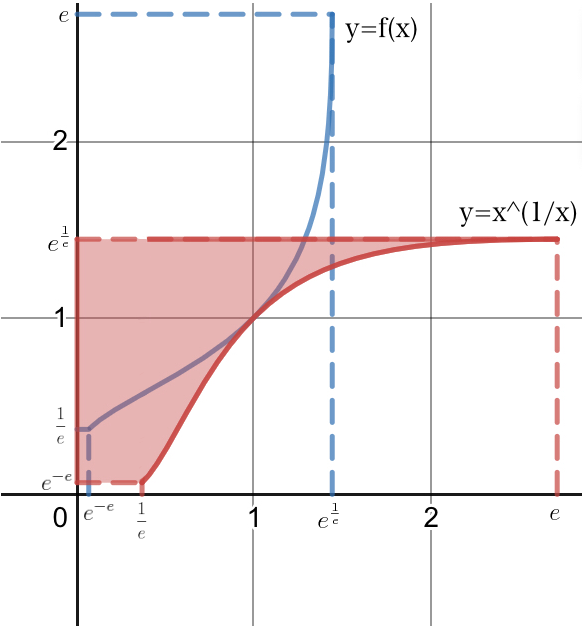
グラフより、赤い部分の面積は以下のように求まります。

(赤い部分の面積) $=$ ( $e\times e^{\frac{1}{e}}$ の長方形) $-$ ( $\frac{1}{e}\times e^{-e}$ の長方形) $-$ ( $y=x^{\frac{1}{x}}$ の $\frac{1}{e}\leqq x \leqq e$ での面積)

よって

$\displaystyle \int_{e^{-e}}^{e^{\frac{1}{e}}} x^{x^{x\cdots}} dx=e^{\frac{1}{e}+1}-e^{-e-1}-\int_{\frac{1}{e}}^{e}\sqrt[x]{x}\,dx$

となります。これをDesmosで数値計算すると、以下のような結果となりました。

別のアプローチ

冒頭で紹介した収束値 $\displaystyle x^{x^{x\cdots}}=\frac{W(-\ln x)}{-\ln x}$ を用いて計算してみます。

つまり、 $\displaystyle\int_{e^{-e}}^{e^{\frac{1}{e}}}\frac{W(-\ln x)}{-\ln x}\,dx$ を求めるわけですが、ランベルトのW関数 $W(x)$ はDesmosに実装されていないし、Wolfram Alphaにこの式をそのままぶち込むとエラーを吐くので、置換します。

以下の $W(x)$ の性質を用います。

$W(x)e^{W(x)}=x,\,W(e)=1,\, W(-1/e)=-1$

いずれも $W(x)$ の定義より明らかです。

$t=W(-\ln x)$ とすると、 $-\ln x=te^t\,\Leftrightarrow\,\displaystyle x=e^{-te^t}$ となります。

$W(-\ln e^{-e})=W(e)=1,\,W(-\ln e^{\frac{1}{e}})=W(-1/e)=-1$ なので、
積分区間は $e^{-e}\rightarrow e^{\frac{1}{e}}$ から $1\rightarrow -1$ となります。よって、

$\begin{align}\displaystyle\int_{e^{-e}}^{e^{\frac{1}{e}}}\frac{W(-\ln x)}{-\ln x}\,dx&=\int_1^{-1} \frac{t}{te^t}(e^{-te^t})'\,dt\\ &=\int_1^{-1} \frac{t}{te^t}(-(1+t)e^{t-te^t})\,dt\\ &=\int_{-1}^1 (1+t)e^{-te^t}\,dt\end{align}$

となります。
これならば、以下のようにDesmosやWolfram Alphaでも計算可能です。
逆関数を用いて計算したときの値と一致していますね。

また、前回求めた公式を使うと以下のように表せます。

$\displaystyle{\int_{e^{-e}}^{e^{\frac{1}{e}}} x^{x^{x\cdots}} dx\\=e^{\frac{1}{e}+1}-e^{-e-1}-\int_{\frac{1}{e}}^{e}\sqrt[x]{x}\,dx\\ =e(e^{\frac{1}{e}}-1)+\frac{1}{e}(1-e^{-e})-\sum_{n=1}^\infty\sum_{k=0}^{n+1}\frac{(-1)^ke^n-e^{-n}}{k!n^{n+2-k}}\\ =e(e^{\frac{1}{e}}-1)+\frac{1}{e}(1-e^{-e})-\sum_{n=1}^\infty\frac{\Gamma(n+2,-n)-\Gamma(n+2,n)}{n^{n+2}(n+1)!}\\ =e(e^{\frac{1}{e}}-1)+\frac{1}{e}(1-e^{-e})-\sum_{n=1}^\infty\frac{1}{n^{n+2}(n+1)!}\int_{-n}^nt^{n+1}e^{-t}dt\\ \approx 1.24413130065}$

一般化

最初の逆関数を用いた求め方には、実は以下の関数等式が背景にあります。

$\displaystyle{\int_b^cf(x)\,dx+\int_{f(b)}^{f(c)}f^{-1}(y)\,dy=cf(c)-bf(b)}$

この等式を利用すると、積分範囲を一般化することが出来ます。

先程と同様に $f(x)=x^{x^{x\cdots}}$ とすると、 $f^{-1}(x)=\sqrt[x]{x}$

$f(x)$ の値域及び $f^{-1}(x)$ の定義域は $\frac{1}{e}\leq x\leq {e}$

$a$ を実数 $(\frac{1}{e}\leq a\leq {e})$ とすると
$f^{-1}(a)=a^\frac{1}{a}$ より、 $f(a^\frac{1}{a})=a$
$f^{-1}(\frac{1}{a})=a^{-a}$ より、 $f(a^{-a})=\frac{1}{a}$

$b=a^{-a},\ c=a^\frac{1}{a}$ を等式に代入すると

$\displaystyle{\int_{a^{-a}}^{a^\frac{1}{a}}x^{x^{x\cdots}}\,dx+\int_{\frac{1}{a}}^{a}\sqrt[y]{y}\,dy=a^\frac{1}{a}\cdot a-a^{-a}\cdot \frac{1}{a}}$

すなわち

$\displaystyle{\int_{a^{-a}}^{a^\frac{1}{a}}x^{x^{x\cdots}}\,dx=a^{\frac{1}{a}+1}-a^{-a-1}-\int_{\frac{1}{a}}^{a}\sqrt[x]{x}\,dx}$
　 $(\frac{1}{e}\leq a\leq {e})$

となります。